Catégories
- Solutions de manutention simples et ergonomiques
- Solution de confort et de recyclage au quotidien
- Panneaux d'affichage configurables et ses accessoires
- Tableaux Totems Multifaces : 3, 4 5 ou 6 faces rotatifs magnétiques sur roulettes
- Porte documents
- Bandes magnétiques
- Marquage par rubans adhésifs ou pochoirs
- Séquenceur, lanceur Kanban et tableau FIFO
- Signalétique : Panneaux et Plaques de porte
- Jeux pédagogiques Lean
- Goodies lean et Lean-6sigma
- Sécurité des biens et des personnes
- Outils Animation Lean
- Sur-mesure
Test de Student pour données appariées
Le test permet de comparer des moyennes d’échantillons dont les données sont appariées.
Introduction
L’appariement permet d’écarter le risque de mauvaise interprétation dans le cas où des données ont des relations communes qui peuvent influer sur les résultats des essais. Dans ce cas spécifique, le test de Student permet de :
- Comparer la moyenne de 2 échantillons
- Comparer la Variance de 2 échantillons (là où pour des données indépendantes, nous utilisions le test de Fisher)
Exemple :
On veut tester un avant/après sur la consommation de viande sur une année d’un même échantillon d’individu. L’appariement s’effectue par l’individu dont les caractéristiques peuvent évoluer entre l’essai 1 et l’essai 2.
On souhaite tester si un plan de formation a été efficace. On comparera les compétences avant et après la formation, l’appariement s’effectuant par les individus ayant suivi la formation.
Le principe
Le principe du test repose sur la création des paires de données. C’est la différence entre les valeurs de cette paire de données que nous allons étudier dans le cas d’une comparaison de moyennes.
Pour la comparaison de variances, nous allons effectuer le test à partir de la corrélation que nous avons entre les variances des 2 échantillons.
Étape 1 : Hypothèse de test
Comparaison de 2 moyennes
Le test consistant à comparer des moyennes, on forme les hypothèses suivantes :
H : μ1 = μ2
H1 : μ1≠ μ2
Comparaison de 2 variances
Le test consistant à comparer des variances, on forme les hypothèses suivantes :
H : σ1 = σ2
H1 : σ1≠ σ2
Étape 2 : Transformer les données
Comparaison de 2 moyennes
On forme une nouvelle donnée qui est :
di = xi1 – xi2
Comparaison de 2 variances
On utilise le rapport entre les 2 variances des échantillons, mais modifiées du coefficient de corrélation de Pearson. Pour le calculer, on utilise deux nouvelles variables :
Ui = Xi1 + Xi2
Vi = Xi1 – Xi2
A partir ces données, on calcule le coefficient de corrélation de Pearson qui sera par la suite tester.
Étape 3 : Valeur pratique
Comparaison de 2 moyennes
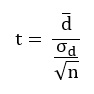
Avec :
- dbarre : moyenne de l’ensemble di des paires de données
- n : nombre de paires d’individu au total
- σd : écart type des différences di
Comparaison de 2 variances
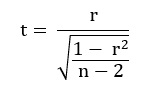
Avec :
- r : coefficient de corrélation de Pearson
- n : nombre de paires d’individu au total
Étape 4 : Calculer la Valeur critique
On utilise l’approximation de la loi de Student pour calculer la valeur critique (fonction Excel LOI.STUDENT.INVERSE.N) pour :
Une probabilité qui va dépendre du sens du test soit :
- Bilatéral : 1 – α/2
- Unilatéral Gauche : α
- Unilatéral Droite : 1-α
Un nombre de degrés de liberté de n-1 (n étant le nombre de paires de données).
Étape 5 : Calculer la p-Value
La p-Value dépend de la taille des échantillons et du sens du test. On utilise la p-Value calculée à partir de la loi de Student. On retrouve ainsi :
- Pour un test bilatéral : LOI.STUDENT ( I valeur pratique I ; ddl ; 2)
- Pour un test unilatéral gauche ou droite : LOI.STUDENT ( I valeur pratique I ; ddl ; 1)
Avec :
- Pour une comparaison de moyenne : ddl = n – 1
- Pour une comparaison de variance : ddl = n – 2
- n : nombre de paires de données
Étape 6 : Interprétation
| Sens du test | Résultat | Conclusion statistique | Conclusion pratique |
|---|---|---|---|
| Bilatéral | Valeur pratique > Valeur critique α/2etValeur pratique < Valeur critique 1 - α/2 | On rejette H0 | Les 2 échantillons sont différents au niveau de risque α donné. |
| Unilatéral droit | Valeur pratique < Valeur critique α | On rejette H0 | L'échantillon 1 est statistiquement plus grand que l'échantillon 2 au niveau de risque α donné. |
| Unilatéral gauche | Valeur pratique > Valeur critique α | On rejette H0 | L'échantillon 1 est statistiquement plus petit que le 2 au niveau de risque α donné. |
| Résultat | Conclusion statistique | Conclusion pratique |
|---|---|---|
| p-value > α | On retient H0 | Nos 2 séries de données sont identiques ou proches avec un risque de se tromper de p-value% |
| p-Value < α | On rejette H0 | Nos 2 séries de données sont statistiquement différentes avec un risque de se tromper de p-value% |
Source
R. Rakotomalala (2013) – Comparaison de populations, tests paramétriques
E. G. Pitman (1939) – A note on normal correlation
A. Myers, C. H. Hansen (2003) – Psychologie expérimentale
M. Vaubourdolle (2007) – Toxicologie, sciences mathématiques, physiques et chimiques



