Catégories
- Solutions de manutention simples et ergonomiques
- Solution de confort et de recyclage au quotidien
- Panneaux d'affichage configurables et ses accessoires
- Tableaux Totems Multifaces : 3, 4 5 ou 6 faces rotatifs magnétiques sur roulettes
- Porte documents
- Bandes magnétiques
- Marquage par rubans adhésifs ou pochoirs
- Séquenceur, lanceur Kanban et tableau FIFO
- Signalétique : Panneaux et Plaques de porte
- Jeux pédagogiques Lean
- Goodies lean et Lean-6sigma
- Sécurité des biens et des personnes
- Outils Animation Lean
- Sur-mesure
Les cartes de contrôles
Les cartes de contrôles sont des outils historiques du SPC (Statistical Process Control). Elles permettent de surveiller les paramètres d’un processus pour prévenir des dérives et s’assurer la qualité.
Introduction
Les cartes de contrôle ont été développées par l'ingénieur W. A. Shewhart dans les années 1920. À cette époque, le management de l'usine de Hawthorne de la Western Electric Company cherchait à améliorer l'uniformité de leurs produits afin de fidéliser leurs clients. Cependant, ils se sont rendu compte que leurs efforts n'aboutissaient qu'à une détérioration de la situation.
Pour remédier à cela, ils ont fait appel au Dr. Shewhart, qui travaillait alors au Bell Telephone Laboratories. Dans le but de réduire les risques en minimisant les erreurs, Shewhart a créé les cartes de contrôle. Son principe repose sur la distinction entre la variabilité aléatoire naturelle d'un processus et la variabilité accidentelle. L'idée n'est pas d'éliminer complètement la variabilité, mais de la mesurer et de la maîtriser.
Le concept clé des cartes de contrôle est de conduire un processus à un état de "contrôle statistique", où seules les variations naturelles sont présentes, afin de prédire les résultats et de gérer le processus efficacement. Ces cartes permettent de distinguer les variations "normales" des variations "exceptionnelles" du processus, et elles répondent aux questions suivantes : "Est-ce que mon processus a changé ?" et "Mon processus est-il stable et prédictible ?"
En résumé, les cartes de contrôle sont un outil puissant pour maintenir la stabilité et la prédictibilité d'un processus, en identifiant et en traitant rapidement les variations indésirables. Elles jouent un rôle crucial dans l'amélioration continue et l'assurance qualité au sein d'une organisation.
Principe
Les cartes de contrôle sont des outils visuels qui permettent de surveiller et de contrôler l'évolution des paramètres d'un processus dans le temps. Elles consistent à prélever régulièrement des échantillons et à représenter les données sur un graphique. On reporte ensuite sur un graphique les données en construisant :
- Une ligne centrale qui représente la moyenne des échantillons. Elle permet d'identifier la "localisation" du processus, c'est-à-dire sa position moyenne.
- Des limites supérieure et inférieure, placées à équidistance de la ligne centrale, à une distance de 3σ (écart-type) de la moyenne. Ces limites définissent une plage de variation acceptable pour le processus.
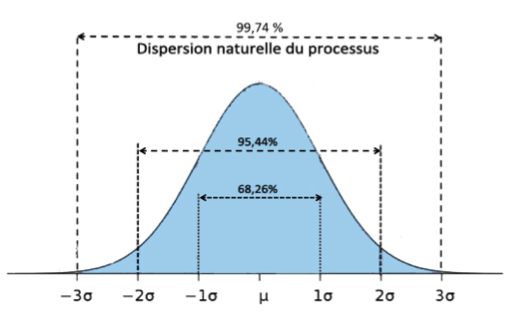
En observant les données sur la carte de contrôle, on peut détecter des décrochages, des évolutions ou des variations significatives par rapport à la norme établie. Si les points se situent en dehors des limites, cela peut indiquer des problèmes ou des variations anormales dans le processus.
Les cartes de contrôle permettent donc de mesurer le niveau de variabilité du processus et de prendre des mesures correctives dès que des variations indésirables sont identifiées. Elles sont un outil essentiel pour maintenir la stabilité et la prédictibilité d'un processus, en permettant une surveillance continue et en facilitant la prise de décisions basées sur des données concrètes.
En résumé, les cartes de contrôle fournissent une représentation visuelle des données d'un processus, avec une ligne centrale représentant la moyenne et des limites supérieure et inférieure définissant la plage de variation acceptable. Elles permettent de détecter les variations anormales et de prendre des mesures pour maintenir le processus sous contrôle.
Pourquoi les limites sont-elles à 3σ ?
Les limites des cartes de contrôle sont généralement établies à 6σ pour plusieurs raisons essentielles. Statistiquement, cette valeur correspond à une probabilité très élevée de 99,99967% d'inclure les valeurs attendues à l'intérieur de cet intervalle. En d'autres termes, il y a seulement 0,000333% de chances que la prochaine valeur se situe en dehors de ces limites.
Bien que cette valeur puisse sembler "arbitraire" à première vue, l'expérience acquise au fil des décennies prouve que ce choix est justifié. Les limites à 3σ sont basées sur l'observation empirique de nombreux graphiques de contrôle et leur utilisation continue a confirmé leur efficacité dans la détection des variations significatives.
W. Edwards Deming, un expert renommé en gestion de la qualité, a souligné que les limites de contrôle ne doivent pas être associées à la recherche de problèmes ou de causes spéciales. Elles servent plutôt à établir un seuil de confiance pour détecter les variations naturelles du processus. L'utilisation de limites à 3σ a été validée par plus de 50 ans d'expérience pratique, démontrant ainsi la pertinence de ce choix.
Pourquoi parle t’on de décalage de 1,5 ?
Dans le cadre des cartes de contrôle, si l’on traduit les DPMO en valeur de σ, on retrouve 1,5 dans la formule. Son origine s’explique par la précision des cartes de contrôles. En effet, en pratique, un process respectant le 6σ à court terme peut ne pas l’être à long terme, et serait donc de 4,5σ.
Les 2 types de variations
Variation naturelle due à des causes communes
Chaque processus présente inévitablement une variabilité naturelle, également appelée "bruit", qui ne peut jamais être totalement éliminée. L'objectif est de réduire et de maîtriser cette variabilité. Elle résulte de l'accumulation d'un grand nombre de petites causes incontrôlables, connues sous le nom de causes communes ou aléatoires.
Les causes communes peuvent être variées et inclure des problèmes d'organisation tels que le manque de formation, le manque d'encadrement, les problèmes de communication ou les procédures obsolètes. Elles peuvent également être liées à des machines ou des produits inadaptés à la situation, comme une conception défectueuse, un mauvais état de la machine, des vibrations, un processus non conforme aux exigences ou de mauvais réglages. Les mauvaises conditions de travail, telles que le manque d'éclairage, les vibrations, l'humidité, les zones de travail encombrées, les problèmes d'ergonomie ou d'approvisionnement, peuvent également contribuer aux causes communes.
Il est intéressant de noter que selon W. Edwards Deming, environ 94% des problèmes rencontrés sont en réalité des variations "naturelles" des processus. En d'autres termes, selon Deming, la majorité des problèmes sont liés à des problèmes de gestion plutôt qu'à des problèmes de qualité.
Variation accidentelle due à des causes spéciales
La variation accidentelle que l’on nome « signal » est une variation exceptionnelle. Elles sont la conséquence des causes spéciales (assignables) et dont on sait en retrouver la source.
Les sources de ces variations sont diverses allant de l’erreur humaine au problème de qualité de la matière en passant par la panne… Tout l’enjeu est de les identifier pour les supprimer.
1. Choisir des paramètres de contrôle
Les paramètres doivent être suffisamment pertinents pour faire en sorte de piloter les processus de manière efficace. Il y a différents critères de choix :
- La simplicité : le paramètre doit être facile à mesurer. Effectuer le prélèvement ne doit pas prendre trop de temps, et le personnel doit être capable de le faire.
- L’importance vis-à-vis du client : on aura plus intérêt à choisir un paramètre qui peut avoir un impact direct sur la qualité pour le client.
- La centralisation : dans certain cas, les paramètres peuvent être corrélés. Si le premier n’est pas conforme, alors les autres ne le seront pas. On a tout intérêt à choisir le paramètre central qui permet d’effectuer le moins de prélèvements, tout en ayant le maximum d’informations.
- L’historique : il y a peu d’intérêt à mettre sous surveillance un paramètre qui ne nous a jamais posé problème. Il sera plus pertinent de mettre sous contrôle un paramètre que l’on sait être problématique.
- Le type de données : statistiquement, il est toujours préférable d’effectuer un relevé sur des données quantitatives (un poids, un diamètre…) plutôt que des données qualitatives (bon, pas bon…). Autant que faire se peut, privilégier ce type de variable qui permet l’utilisation de cartes plus performantes.
2. Mettre en place le mode d’échantillonnage
Comme dans toute procédure de relevée de données pour effectuer des statistiques, il faut respecter les processus de base des plans d’échantillonnage.
2.1 Le mode de prélèvement
Dans le cas spécifique des cartes de contrôles, notre plan d’échantillonnage s’appuie sur une méthode probabiliste aléatoire. On effectue alors un tirage aléatoire selon 2 méthodes :
Prélèvement à intervalle de temps régulier (exemple : on prélève 5 échantillons toutes les heures, quelque soit la quantité produite sur la dernière heure) : on utilise cette approche pour suivre réellement l’évolution du processus
Prélèvement en fonction de la quantité produite (exemple : on prélève 5 échantillons toutes les 1000 pièces produites (ou tous les lots de production)) : on utilise cette approche dans le cas où l’une des finalités du suivi vise à l’acceptation ou non des lots de production.
2.2 Calcul de la taille de l’échantillon
Historiquement, la taille d'un échantillon pour les cartes de contrôle était fixée à 5. Cette valeur était pratique car elle permettait de calculer facilement la moyenne en multipliant par 10 et en divisant par 2.
Il est généralement recommandé de prélever 4 ou 5 échantillons dans chaque sous-groupe pour deux raisons principales. Premièrement, pour que les relevés soient représentatifs, les prélèvements doivent être effectués dans un laps de temps réduit afin d'éviter les changements qui pourraient influencer les résultats du processus. Deuxièmement, d'un point de vue pratique, plus le nombre d'échantillons est élevé, plus cela engendre des coûts supplémentaires.
Il est important que la taille de l'échantillon reste constante à chaque prélèvement. Dans le cas contraire, la taille du plus grand échantillon ne doit pas dépasser deux fois la moyenne, et la taille du plus petit échantillon ne doit pas être inférieure de plus de deux fois la moyenne. Pour les cartes de contrôle proportionnelles, la taille de l'échantillon ne doit pas varier de plus de 25% par rapport à la taille de référence.
Cependant, la détermination de la taille de l'échantillon optimale dépendra de la pratique et de l'expérience. Par exemple, dans les cas où la variabilité est très faible (moins d'un écart-type), les cartes de contrôle peuvent manquer de sensibilité pour détecter de si petites variations. Dans de tels cas, il est nécessaire d'avoir une taille d'échantillon suffisamment grande pour les détecter.
2.3 Fréquence de prélèvement
Pour déterminer la fréquence, des spécialistes ont définis des abaques. Toutefois, on préférera l’empirisme pour la déterminer. Elle dépend du niveau de qualité attendu et du niveau actuel, de la cadence de production, de la fréquence des réglages, pannes… Et d’une manière générale, des moyens que l’on souhaite mettre en œuvre.
Néanmoins, en première approche, on utilise la règle de Cavé. Principalement lié à la fréquence des réglages réels, cette règle permet de se donner une première base de réflexion. La formule suivante :
Pour une production à forte cadence*
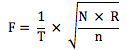
Pour une production à faible cadence* ou production continue
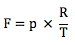
Avec :
T : temps prit en compte pour le calcul
N : Nombre de pièces produites sur l’unité de temps T
n : taille d’un échantillon à prélever
p : nombre moyen d’échantillons prélevés entre 2 réglages successifs
R : nombre moyen de réglage sur l’unité de T
*A noter que pour définir si notre production est à forte ou faible cadence, la condition est la suivante :
Si N > p² * n * R : Forte cadence
Si N < p² * n * R : Faible cadence
D’autres conventions sont à ne pas omettre comme cette règle basée sur l'expérience selon laquelle les actions correctives sur un processus doivent être au moins 4 fois moins fréquentes que la fréquence de prélèvement. Cela permet de maintenir un équilibre entre la surveillance du processus et les efforts de correction.
Dans le cas de productions à très faible cadence, si la fréquence de prélèvement estimée selon la règle de Cavé conduit à contrôler plus de 50% de la production, il peut être nécessaire d'effectuer un contrôle à 100%. Cependant, dans la plupart des cas, il est préférable de commencer avec une fréquence de prélèvement plus élevée et de la réduire progressivement à mesure que des améliorations sont apportées au processus.
Exemple :
| Vérin à gaz | Lots de produits pharmaceutiques | Avion | Produit chimique | |
|---|---|---|---|---|
| Cadence moyenne N | 10 000 /semaine | 190/mois | 30 par mois | Indéterminé |
| Temps pris en compte T | 7 jours | 20 jours | 20 jours | 30 jours |
| Nombre moyen de réglage R | 14/semaine | 6/mois | 4 par mois | 8 par mois |
| p choisi arbitrairement | 4 | 4 | 4 | 5 |
| Taille d'échantillon | 5 | 3 | 1 | 6 |
| Type de cadence | p²nR=1120 < N ⇒ Production à forte cadence | p²nR=288 > N ⇒ Production à faible cadence | p²nR=48 > N ⇒ Production à faible cadence | Production continue |
| Fréquence calculée de prélèvement F | 1710000 x 145 = 23,9 | 4 x 620 = 1,2 | 4 x 330 = 0,8 | 5 x830 =1,33 |
| Fréquence choisie | 1 échantillon /heure | 1 échantillon/jour | - | 2 échantillons/jours |
| % de production contrôlé | 8,4% | 47,4% | Nous sommes à 80% de fréquence calculée, donc contrôle à 100% | N/A |
2.4 Valider le recueil
Il faut s’assurer que les données prélevées soient fiables auquel cas, le résultat n’en sera que moins bon. Pour cela, on effectue une étude Gage R&R ou un Kappa Test.
2.5 Valider la distribution des données
Les cartes de contrôles sont construites sur l’hypothèse de normalité des données. Pour s’assurer d’interpréter correctement les résultats, il est nécessaire de s’assurer de cette condition :
- En effectuant un test d’ajustement à la loi normale
- En dessous de 4 échantillons par sous-groupes, la validation de l’hypothèse de normalité est importante.
- Au delà de 4 échantillons par sous-groupes, l’hypothèse de normalité peut être considérée comme « valide ».
3. Choisir la carte
| Cartes aux mesures | Cartes aux attributs | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Type de contrôle | Moyenne à grande série et pour des paramètres quantitatifs | Compter le nombre de rebut dans chaque échantillon : valeur binaire Bon / Pas Bon | Compter le nombre de défauts, un même produit pouvant avoir plusieurs défauts | ||||||||
| Taille de l’échantillon | 1 et + | 1 | 2 à 25 | + de 6 | Plusieurs centaines de préférence, mais quelques dizaines si on ne peut faire mieux | ||||||
| Type d’échantillon | Variable | Constante | Variable | Constante | Variable | Constante | Variable | ||||
| Sensibilité | < 1σ | 1σ | > 1,5σ | 1σ | < 1σ | ||||||
| Déréglage | Lent | Rapide | Lent | ||||||||
| Nom de la carte | CUSUM aux mesures | EWMA aux mesures | I-mR | Xbar-R | Xbar-S | NP | P | C | U | CUSUM aux attributs | EWMA aux attributs |
*La sensibilité est le niveau de performance d’une carte. Plus la sensibilité est faible, et plus la carte est performante. Elle sera en effet capable de détecter des dérives plus faibles et donc d’alerter au plus tôt qu’un problème apparaît.
On note qu’il existe d’autres types de cartes : carte Shainin, carte χ, carte de Robert-Shiriaev, carte FMA ou encore carte T (Hotelling).
4. Construire la carte
La construction des cartes de contrôle suit un processus strictement similaire, avec la présence d'une valeur centrale et de deux limites. Les différences résident dans les formules utilisées pour calculer ces valeurs.
La construction des cartes se déroule en deux phases distinctes :
Phase I : Cette phase est utilisée lorsque nous n'avons pas encore suffisamment de données pour effectuer des calculs fiables. Pour les cartes de contrôle aux mesures, cela correspond généralement à moins de 15 données ou groupes de données. Pour les cartes de contrôle aux attributs, la norme X06-032-1 recommande d'utiliser cette phase jusqu'à un minimum de 300 données.
Phase II : Une fois que nous disposons statistiquement d'un nombre suffisant de données, nous entrons dans la phase II. À ce stade, nous pouvons nous assurer que les données suivent approximativement une distribution normale.
Il est important de noter que l'interprétation et les actions à entreprendre varient en fonction de la phase de la carte :
- Les cartes de la phase I ne permettent pas de tirer de conclusions ni d'entreprendre des actions spécifiques. Elles nécessitent davantage de données pour être fiables.
- Seules les cartes de la phase II sont considérées comme fiables et appropriées pour l'interprétation et la prise de décisions.
5. Interpréter une carte de contrôle
On crée différentes zones sur le graphique. On rajoute des lignes à 1 et 2σ au dessus et en dessous de la ligne médiane, et on défini les zones comme dans le graphique ci-contre.
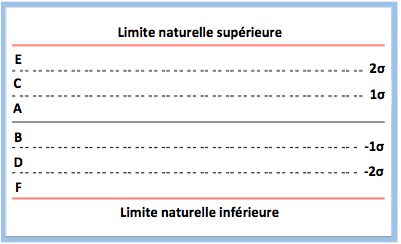
5.1 – Les critères pour « ne pas agir »
La « forme » idéale d’une carte de contrôle doit répondre aux critères suivants :
- 2/3 des points sont dans les zones A et B.
- Peu de points sont dans les zones E et F.
- Les points sont également répartis au dessus et en dessous de la ligne moyenne.
- Il n’y a pas de points en dehors des limites de contrôle.
La première signification d’un profil normal est que le processus est sous contrôle. Il est stable et n’est pas perturbé par des causes extérieures. Il tend à se répéter jour après jour, et par conséquent il est prévisible. On peut déterminer, par le calcul, les caractéristiques sous-jacentes : le centre, la forme et la dispersion de la distribution.
5.2 – Les critères pour « agir »
Un profil « anormal » indique que le processus est hors contrôle. Il n’est pas prévisible.
Même si les critères pour identifier un profil anormal sont identiques pour toutes les cartes, l’interprétation diffère en fonction du type de carte. Nous décrivons ci-dessous les critères, mais nous indiquons uniquement une « règle » générale d’action à effectuer.
Ci-dessous, nous retrouvons les 8 critères définis selon la Western Electric. L’ordre d’importance dans lequel ils sont mis est par contre celui défini par Nelson, indiquant les principes suivants :
- Les règles 1 à 4 sont applicables tout le temps. Le risque de voir un événement alors qu’il n’y en a pas est de l’ordre de 1%.
- Les règles 5 et 6 sont à appliquer s’il est économiquement viable d’avoir une alarme le plus tôt possible. Mais la probabilité de voir un événement alors qu’il n’y en a pas est de 2%.
- Les règles 7 et 8 sont intéressantes pour la mise en place des cartes. Le test 7 réagit toujours lorsque les variations proviennent de 2 populations, alors que le test 8 réagit lorsque les variations proviennent d’une même population.
| Description | Probabilités d'action | Type d'action | Aspect de la carte de contrôle | |
| Critère 1 | Un point est à l'extérieur des limites | 2,7 pour 1000 | Une action immédiate de réglage est nécessaire | 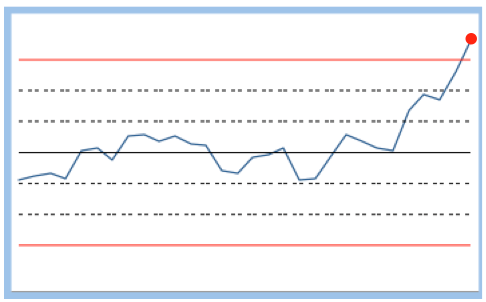 |
| Critère 2 | 9 points de suite du même côté de la ligne médiane | 3,91 pour 1000 | Un réglage est nécessaire pour recentrer le processus | 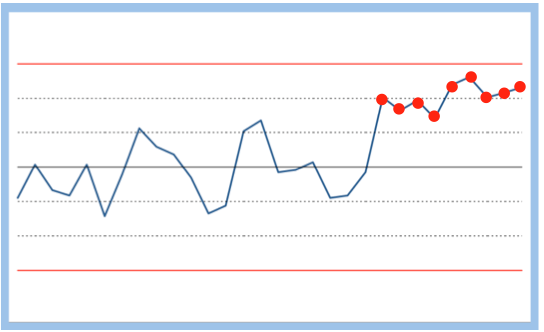 |
| Critère 3 | 6 points de suite croissant ou décroissant | 2,78 pour 1000 | Une dérive du processus se fait sentir sans doute dû à un élément qui se déteriore. Il faut le rechercher pour le réparer | 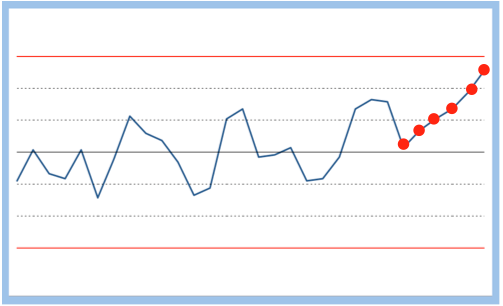 |
| Critère 4 | 14 points de suite passent tour à tour de bas en haut | 4,57 pour 1000 | La situation est anarchique, il y a un manque clair de contrôle | 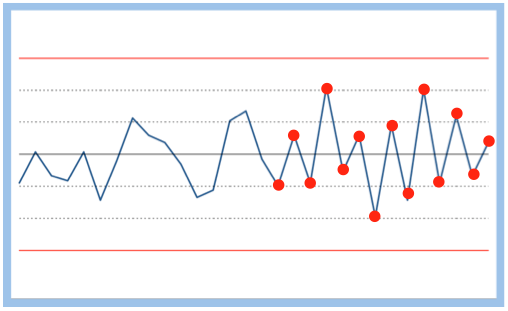 |
| Critère 5 | Parmi les 3 derniers points, 2 se retrouvent en zone E ou F | 3,06 pour 1000 | Un nouveau prélèvement est nécessaire pour voir si le processus revient entre -2σ et 2σ. Si ce n'est pas le cas, un réglage sera nécesaire | 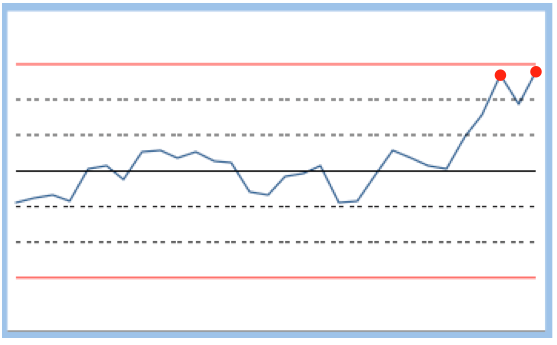 |
| Critère 6 | Parmi les 5 derniers ponts, 4 se retrouvent en zone C ou D ou au-delà | 5,53 pour 1000 | Il y a beaucoup de dispersion dans le processus. Une "future" panne en est sans doute à l'origine | 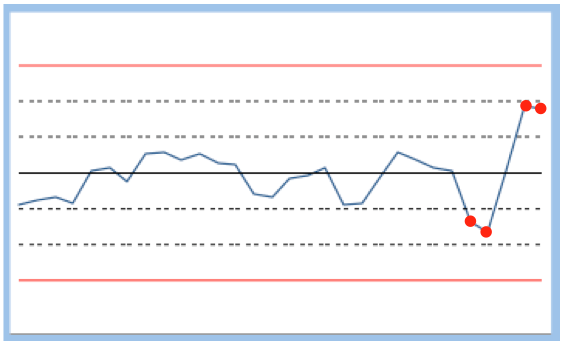 |
| Critère 7 | 15 points d'affilés à l'interieur de la zone AB | 3,26 pour 1000 | Il serait intéressant de faire un test t pour comparer l'échantillon des 15 points précédents pour savoir si nous n'avons pas 2 groupes de données distincts permettant de dire que des actions de progrès ont porté leurs fruits | 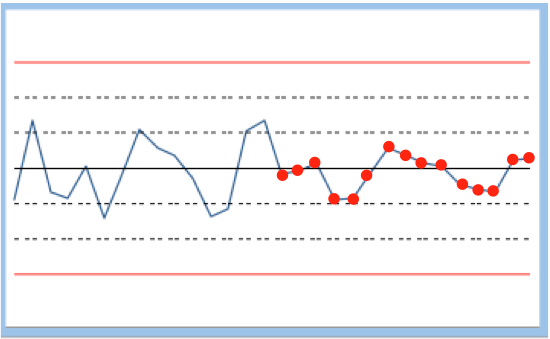 |
| Critère 8 | 8 points de suite situés des 2 côtés de la ligne centrale mais aucun en zone AB | 0,1 pour 1000 | Il ya beaucoup de dispersion. Il devient nécessaire d'agir et trouver la cause | 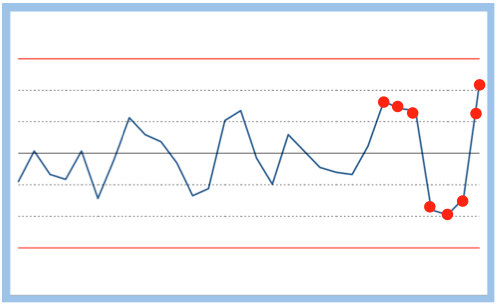 |
Dans tous les cas, lorsqu’une de ces situations est mise en avant, il faut refaire un prélèvement dans l’immédiat. Pour valider la situation, il faut que le résultat de celui-ci soit dans la zone AB.
Dans le cas contraire, il faut investiguer sur les causes dans l’immédiat.
Les autres règles :
Selon la norme NF X06-031
- Un point est à l’extérieur des limites.
- 9 points de suite du même côté de la ligne médiane.
- 6 points de suite croissant ou décroissant.
- Parmi les 3 derniers points, 2 se retrouvent en zone E ou F.
Selon l’AIAG
- 1 point en dehors des limites.
- 7 points consécutifs sont en dessous ou au dessus de la ligne médiane.
- 7 points consécutifs sont croissants ou décroissants.
Selon Juran
- 1 point en dehors des limites.
- Parmi les 3 derniers points, 2 se retrouvent en zone E ou F
- Parmi les 5 derniers points, 4 se retrouvent en zone C ou D ou au delà.
- 6 points de suite croissant ou décroissant.
- 9 points de suite du même côté de la ligne médiane.
- 8 points de suite situés des 2 côtés de la ligne centrale mais aucun en zone AB.
Selon Westgard
- Un point est à l’extérieur des limites.
- 2 points d’affilés en zone E ou F.
- 4 points d’affilés en zone C ou D ou au delà.
- 10 points d’affilés du même côté de la ligne médiane.
- Pour 2 points d’affilés, 1 est en zone E et l’autre en F ou au delà.
- 7 points d’affilés croissant ou décroissant.
Le calcul des probabilités d’apparition des règles de NELSON
Cela fait partie des conditions d’utilisation des cartes de contrôles, les données doivent suivre une loi normale. Cette condition est nécessaire, car elle conditionne le fait que les règles pour “agir” soit valide ou non. Au regard de la loi Normale, la probabilité que nos points soient dans une zone spécifique est indiqué dans le schéma suivant :

D’où nous déduisons la probabilité d’apparition de chacune des règles :
- Règle 1 : 2 * probabilité pour hors limite = 2 * 0,135% = 2,7 pour mille
- Règle 2 : 2 * probabilité de A ou B ou C ou D ou E ou F = 2 * (0,13591 + 0,34134 + 0,0214)9 = 3,91 pour mille
- Règle 3 : Probabilité en comptant que l’ordre est important : (1 + 1) / 6! = 2,78 pour mille
- Règle 4 : 398721962 / 14! = 4,57 pour mille
- Règle 5 : 2 * C(2;3) * probabilité de (E ou Limite haute)2 * (1 – Probabilité de E ou limite haute) + 2 * (probabilité de E ou limite haute)3 = 2 * 3 * 0,022752 * 0,97725 + 2 * 0,022753 = 3,06 pour mille
- Règle 6 : 2 * C(4;5) * probabilité de (Limite haute ou E ou C)4 * (1 – probabilité de (Limite haute ou E ou C)) + 2 * (probabilité de Limite haute ou E ou C)5 = (2 * 5 * 0,158654 * 0,84135 + 2 * 0,0158655 = 5,53 pour mille
- Règle 7 : Probabilité de (A ou B)15 = 0,6826815 = 3,26 pour mille
- Règle 8 : probabilité de (limite haute ou E ou C ou D ou F ou Limite basse)8 = 0,317328 = 0,1 pour mille
6. Piloter avec une carte de contrôle
Tout l’intérêt des cartes de contrôle est de fournir aux managers les bons signaux d’actions. Elles permettent d’identifier les « vrais » des « faux » problèmes, de savoir si nos actions ont réellement porté leurs fruits…
On retrouve 2 manières de mal interpréter les cartes de contrôles, que nous détaillons ci-dessous.
Sur-réagir
La surréaction se produit lorsqu'une variation est attribuée à une cause spéciale alors qu'elle est en réalité due à des causes communes. Cela se produit lorsque le processus produit en dehors des spécifications définies par la Voix du Client, mais à l'intérieur des spécifications définies par la Voix du Processus. En d'autres termes, le processus est en réalité non-capable.
La réaction traditionnelle à cette situation consiste souvent à effectuer des réglages ou à entreprendre des actions pour ramener le processus à l'intérieur des spécifications clients. Cependant, cette sur-réaction est inefficace car le problème fondamental réside dans le fait que le processus lui-même n'est pas capable de répondre aux spécifications clients, ou que les spécifications clients sont trop exigeantes.
Il est important de comprendre que des ajustements ou des actions à court terme ne résoudront pas le problème sous-jacent. Dans de tels cas, une analyse plus approfondie du processus et des spécifications clients est nécessaire pour identifier et résoudre les problèmes de capacité du processus.
Sous-réagir
La sous-réaction se produit lorsqu'une variation est attribuée à une cause commune alors qu'elle est en réalité due à une cause spéciale. C'est l'inverse du cas précédent. Les prélèvements indiquent que nous sommes à l'intérieur des tolérances définies par la Voix du Client, mais en réalité, nous nous trouvons en dehors des limites naturelles du processus.
Étant donné que le processus est capable, on ne se rend pas compte qu'il est en train de dériver. Malheureusement, dans de tels cas, aucune action n'est généralement entreprise et on "attend" une défaillance ou un défaut majeur avant d'agir.
Cette sous-réaction est problématique car elle peut conduire à des problèmes graves et à des conséquences négatives pour la qualité et les performances du processus. Il est important d'être vigilant et de prendre des mesures préventives pour prévenir les dérives du processus, même lorsque les variations semblent être à l'intérieur des tolérances.
Et donc…
Pour manager correctement les processus, il faut pouvoir dissocier la Voix du Client et la Voix du Process. Les tolérances clients permettent uniquement de faire le tri entre ce qui est bon de ce qui est mauvais. Autrement dit, elles permettent de juger ce qui a été fait et donc de regarder en arrière.
A l’inverse, les tolérances naturelles du processus permettent de piloter au jour le jour et de réagir au plus tôt pour ne pas produire de défaut. On est dans une attitude proactive.
7. Standardiser et améliorer
Le processus de prélèvement est rentré dans les mœurs. Le processus est optimisé et génère de moins en moins de problèmes. On peut réduire la surveillance et le nombre de prélèvements.
Source
R. W. Berger (2002) – The certified quality engineer handbook
Western Electric (2012) – Manuel du contrôle statistique de la qualité
W. E. Deming (2000) – Out of crisis
F. Boulanger, G. Chéroute, V. Jolivet (2006) – Maîtrise statistique des processus
M. Pillet (2005) – Appliquer la maîtrise statistique des processus
L. Alwan (2000) – Statistical process analysis
C. D. Montgomery (1996) – The ASTM manuel of presentation of data and control chart analysis
E. G. Schilling, P. R. Nelson (1976) – The effect of non-normality on th control limits Xbarre charts
Western Electric (1956) – Statistical quality control handbook
L. S. Nelson (1984) – Technical aids
D. Griffiths, M. Bunder, C. Gulati, T. Onzawa (2010) – The probability of an Out of Control Signal from Nelson’s Supplementary Zig Zag test.
T. Mariani, P. Mariani (2012) – Juggling paradigms, exemple d’un déroulement de projet Six Sigma de A à Z
W. Shewhart (1931) – Economic control of quality of manufacturing product
D. Howard (2004) – The basics of statistical process control & process behaviour charting
S. Mayeur (2004) – Guide opérationnel de la qualité
F. A. Meyer (2014) – Appliquer la ToC Lean Six Sigma dans les services
H. Toda (1958) – Band-score control charts
P. R. Bertrand (2007) – Une introduction au contrôle qualité
Norme NF X06-031-0 – Cartes de contrôle, Partie 0 : Principes généraux



