Introduction
Le test de la loi binomiale est le test de la chance par excellence qui est à l’origine des calculs probabilités. Elle est née en 1713 avec la publication de "Ars conjectandi", l’œuvre posthume du Suisse Bâlois Jacob Bernoulli.
Le principe
Chaque tirage a la probabilité p d’être un succès et la probabilité q = 1 – p d’être un échec. Si la distribution suit la loi théorique binomiale, la probabilité de succès est écrite de la manière suivante :
- n : Le nombre de tirage au total
- k : Le nombre de succès que nous voulons voir parmi nos n tirages
- P : La probabilité de succès
- q : la probabilité d’échec
Sa moyenne = n * p
Sa variance = n * P * (1 – p)
Probabilité d’un évènement
La loi binomiale est utilisée pour calculer la probabilité qu’un événement se produise dans le cas où :
- l'ordre n'a pas d’importance.
- A chaque tirage, nous remettons l’élément que nous venons de tirer.
Nous sommes donc dans le cas 2 du calcul de probabilités "sans ordre, avec remise".
L’exemple le plus typique est le résultat du dé. Pour obtenir au moins 3 fois le nombre 6 lancers sur 4, notre probabilité de ce calcul est la suivante :
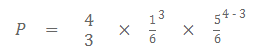
Soit 1,54% de chance d’avoir notre succès. Résultat qui peut être trouvé dans Excel en utilisant la fonction binomiale : LOI.BINOMIALE (k;n;1/6;0).
Il convient de noter que plus notre population est grande (de N = 100), plus la loi binomiale se rapproche de la Loi Hypergeométrique, d’où le fait que l’approximation est souvent faite, la loi binomiale étant plus facile à calculer à la fois à la main et à l’aide de tableurs.
Le test d’hypothèse
La loi binomiale peut également être utilisée pour savoir si un nombre d’événements correspond à sa probabilité "à priori" ou non. C’est généralement le cas lorsque l’on veut savoir si un dé est pipé. Nous savons que nous avons une probabilité de 1/6, l’enjeu de ce test sera alors en fonction de notre résultat réel obtenu, pour savoir si le dé est bien "aux normes".
Étape 1 : les hypothèses
Le test binomial peut être un test bilatéral ou unilatéral. Si nous posons p la valeur théorique de p, nous avons les hypothèses suivantes :
Bilatéral
- H0 : p = p0
- H1 : p ≠ p0
Unilatéral gauche
- H0 : p ≠ p0
- H1 : p < p0
Unilatéral droit
- H0 : p ≠ p0
- H1 : p > p0
Étape 2 : calculer la valeur pratique
La valeur pratique est simplement notre pourcentage observé de succès.
Étape 3 : Calculer la valeur critique
La valeur critique dépendra de la direction du test. Il faut donc calculer de la manière suivante pour prendre en compte le risque :
- bilatéral : α/2 et 1 – α/2
- Unilatéral gauche : α
- Unilatéral droit : 1 – α
La fonction Excel est LOI.BINOMIALE.INV.N.
Étape 4 : Calculer la p-value
Pour p-Value, nous utilisons l’approximation de la distribution binomiale, qui sera la même quelle que soit la signification du test. Dans Excel, la fonction est LOI.BINOMIALE.
Étape 5 : Interprétation
| Sens du test | Résultat | Conclusion statistique | Conclusion pratique |
|---|---|---|---|
| Bilatéral | Valeur pratique > + Valeur critique ou Valeur pratique < - Valeur critique | On rejette H0 | Nos données ne suivent pas la loi Binomiale |
| Unilatéral droit | Valeur pratique > Valeur critique | On rejette H0 | Nos données sont au dessus de la loi Binomiale |
| Unilatéral gauche | Valeur pratique < Valeur critique | On rejette H0 | Nos données sont en dessous de la loi Binomiale |
| Résultat | Conclusion statistique | Conclusion pratique |
|---|---|---|
| p-value > α | On retient H0 | Nos données suivent la loi Binomiale |
| p-Value est ≤ α | On rejette H0 | Nos données ne suivent pas la loi Binomiale. |



