Catégories
- Solutions de manutention simples et ergonomiques
- Solution de confort et de recyclage au quotidien
- Panneaux d'affichage configurables et ses accessoires
- Tableaux Totems Multifaces : 3, 4 5 ou 6 faces rotatifs magnétiques sur roulettes
- Porte documents
- Bandes magnétiques
- Marquage par rubans adhésifs ou pochoirs
- Séquenceur, lanceur Kanban et tableau FIFO
- Signalétique : Panneaux et Plaques de porte
- Jeux pédagogiques Lean
- Goodies lean et Lean-6sigma
- Sécurité des biens et des personnes
- Outils Animation Lean
- Sur-mesure
Dans de nombreux cas, nous avons des corrélations claires et pour autant, nous ne savons pas les quantifier car elles sont non linéaires.
Les régressions linéaires simples sont limitées aux cas où les données suivent une logique linéaire Y = aX + b. Cependant, dans de nombreux cas réels, les relations entre les variables peuvent être non linéaires et nécessitent une approche plus flexible.
C'est là que les régressions monotones entrent en jeu. Pour modéliser ces relations non linéaires, on utilise différentes techniques de linéarisation des données X et/ou Y en fonction du type de relation.
1. Identifier visuellement le type de relation
Première étape si nous pensons que la régression est non linéaire, identifier visuellement le type de relation à priori. Pour cela, on construit le nuage de points, puis on recherche parmi l’un des 3 modèles ci-dessous celui qui correspond le mieux à notre situation :
| Nom | Formule | Graphique |
Exponentielle Elle possède une asymptote verticale | 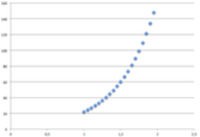 | |
Logarithmique Elle a une asymptote horizontale | 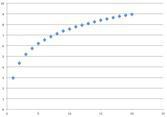 | |
Puissance Elle n’a pas d'asymptote | 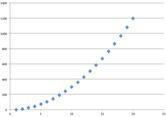 |
2. Linéariser les données
Linéarisation exponentielle
On transforme dans ce cas les données Y. On calcule ln(Y) et on trace le nuage de point ln(Y) en fonction de X. Si notre choix est bon, les points forment une droite.
Linéarisation logarithmique
On transforme dans ce cas uniquement les données de X. On calcule ln(X) et on trace le nuage de point ln(X) en fonction de Y. Si notre choix est bon les points forment une droite.
Linéarisation puissance
On transforme dans ce cas les données X et Y. On calcule ln(X) et ln(Y) puis on trace le nuage de point ln(X) en fonction de ln(Y). Si notre choix est bon les points forment une droite.
3. Calculer la droite de régression linéaire
Nos données étant désormais linéaire, on calcule la droite de régression linéaire associée Y = a * X + b.
4. Déduire la formule de corrélation
Ayant modifié les données initiales, nous allons devoir faire la démarche inverse pour trouver le modèle correspondant à notre situation réelle :
Exponentielle :
![]()
Logarithme :
![]()
Puissance :
![]()
Source
R. Rakotomalala (2013) – Econométrie, la régression linéaire simple et multiple
S. Champely (2004) – Statistique vraiment appliquée au sport
J. M. Azaïs, J. M. Bardet (2012) – Le modèle linéaire par l’exemple
P. Dagnelie (2006) – Statistique théorique et appliquée
W. Fox (1999) – Statistiques sociales



